Ananlisis Regresi Linier
Analisis Regresi Linear
Nama: Qiqit Liana Sari
Kelas 4 psy c
Mata kuliah statistik ekonomi (statistik
II)
Dosen pengampuh Mahardhika Cipta Raharja
S.E., MSi
Jika dalam analisis korelasi hanya menjelaskan tentang bagaimana mengukur kuat dan lemahnya variable
dan untuk memperkirakan arah dan signifikansi hubungan linear antara dua
variable.Namun jika koefisien korelasinya secara signifikan berbeda dari nol maka langkah berikutnya adalah menjabarkan suatu persamaan untuk mengungkapkan hubungan
linear antara dua variable.Persamaan ini disebut dengan analisis regresi. Analisis regresi
linear ini digunakan untuk mengukur apakah antar variable
tersebut saling terikat atau tidak. Bentuk umum dari persamaan regresi linear
tersebut adalah:
Ŷ = a + bX
Ŷ = dibaca Y topi,
adalah perkiraan nilai variabel Y untuksetiapnilai X yang dipilih
X = titikpotong Y. Yakni nilai perkiraan Y
ketika
a = intersep (pintasan) bilamana X=0
b = koefisienarahatau slope garisregresi
Adapunlangkah-langkah yang digunakan untuk menentukan persamaan regresi
linear adalah:
1. Membuat table
penolong untuk memudahkan dalam perhitungan regresi secara manual.
2. Sebagaicontoh table penolong berikut:
No
|
X
|
Y
|
XY
|
X2
|
Y2
|
1
|
…
|
…
|
…
|
…
|
…
|
2
|
…
|
…
|
…
|
…
|
…
|
3
|
…
|
…
|
…
|
…
|
…
|
4
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
…
|
N
|
…
|
…
|
…
|
…
|
…
|
X
|
Y
|
XY
|
X2
|
Y2
|
3. Menghitung niaikonstanta b
4. Mencari nlai a
5. Membuat persamaan regresi
Ŷ = a + bX
Kemudian untuk menggambar garis regresi tersebut dengan menggunakan titik-titik yang kemudian membentuk garis. titik-titik tersebut dapat ditentukan persamaan regresi yakni dengan mengganti nilai X dalam persamaan tersebut.
Garis regresi kuadrat terkecil memiliki ciri tersendiri yang unik dan menarik. pertama, garisnya selalu melalui titik (X.Y). kesdua, tidak ada garis lain yang melalui data yang penjumlahan nilai kuadrat deviasinyya lebi kecil. dengan kata lain Σ(X-Y)2 lebih kecil pada persamaan regresi kuadrat terkecil dibandingkan persamaan lain manapun.
Garis regresi kuadrat terkecil memiliki ciri tersendiri yang unik dan menarik. pertama, garisnya selalu melalui titik (X.Y). kesdua, tidak ada garis lain yang melalui data yang penjumlahan nilai kuadrat deviasinyya lebi kecil. dengan kata lain Σ(X-Y)2 lebih kecil pada persamaan regresi kuadrat terkecil dibandingkan persamaan lain manapun.
Setelah ditentukan persamaan regresi yang telah sesuai dengan data yang didasarkan pada prinsip kuadrat terkecil. pada persamaan regresi sendiri adalah untuk menghubungkan antar variabel.
Langkah selanjutnya adalah melakukan analisa persamaan regresi dengan melakukan uji hipotesis untuk melihat apakah kemiringan regresi berbeda dari nol. hal ini pennting karea jika kita dapat menunjukkan bahwa kemiringan garis pada populasinya berbeda dari nol maka kita menyimpulkan bahwa pengunaan persamaan regresi menambahkan kemampuan kita untuk memperkirakan atau meramal variabel terikat berdasarkan variabel bebasnya. untuk mengujia hipotesis nol, kita menggunakan distribus t dengan (n-k) dengan rumus:
denganderajatkebebasan
n-k
Langkah awal kita adalah menentukan hipotesis nol dan hipotesis alternatifnya:
H0: β ≤ 0
H1 :β> 0
Jikamelakukan hipotesis satu sisi, jika tidak menolak hipotesis nol maka menyimpulkan bahwa kemiringan garis regresi populasi sama dengan nol. hal ini berarti tidak ada hubungan antara variabel terikat dengan variabel bebasnya.
Namun
jika menolak hipotesis nol dan menerima hipotesis alternatifnya maka kita
menyimpulkan bahwa kemiringan garisnya lebih besar dari nol. Dengan demikian,
variabel bebasnya, dapat membantu memperkirakan variabel terikat.
Kesalahan
standar estimasi adalah suatu ukuran yang menunjukkan seberapa tepat prediksi
untuk Y berdasarkan X atau sebaliknya, seberapa tidak akuratnya estimasi itu. Kesalahan
standar esrimasi dilambangkan denganSy.x. Tulisan dibawah garis y.x
ditafsirkan sebagai kesalahan standar dari y untuk setiap nilai x. Konsepnya
sama dengan standar deviasi namun dalam standar deviasi mengukur sebaran di
sekitar rata-ratanya. Sedangkan kesalahan standar estimasi digunakan untuk
mengukur sebaran di sekitar garis regresi untuk setiap nilai x. Untuk
menghitung kesalahan strandar estimasi digunakan rumus :
Jika
kesalahan standar estimasinya kecil, hal ini menunjukkan bahwa data relatif
mendekati garis regresi dan persamaan regresinya dapat digunakan untuk
memperkirakan dengan sedikit kesalahan. Namun jika kesalahan standar
estimasinya besar maka hal ini menunjukkan bahwa data tersebar secara luas di
sekitar garis regresi dan persamaan regresinya tidak akan memberikan estimasi Y
yang tepat.
Dalam
hal ini regresi linear sederhana dapat digunakan untuk mengukur pengaruh antara
variable bebas dengan variable terikatnya ataupun sebaliknya. Untuk mengukurnya
digunakan berbagai cara yakni dengan menggambar garis regresi, dan mengukur
signifikasi kemiringan garis regresi.
Referensi
Lind,
Marchal, dan Wathen.2017.Teknik-teknik Statistika Dalam Bisnis Dan Ekonomi.Jogjakarta:Salemba
Empat.
Rini
Oktofiyani, Nurmalasari, Wakhyu Anggraeni, “Penerimaan Sisten E-Learning
Menggunakan Technology Acceptance Model (TAM) Study Kasus Siswa/I Kelas X di
SMU Negeri 92 Jakarta”, Dimuat Dalam Jurnal Pilar Nusa Mandiri STMIK Nusa
Mandiri Jakarta (Prodi Sistem Informasi),Vol.XIII, No.1, Maret 2016. Dapat
diakses pada http://media.neliti.com
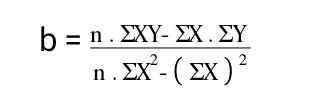






Komentar
Posting Komentar